Estimation sur petits domaines: taux de pauvreté par département
L'estimation de petits domaines est une technique statistique qui permet de répondre aux défis sur la disponibilité des données désagrégées au niveau des collectivités territoriales. En effet, les enquêtes auprès des ménages offrent souvent plusieurs informations détaillées mais, en raison des coûts enormes, ne permettent pas une représentativité des indicateurs jusqu'au niveau le plus fin (départements, communes). Les recensements couvrent tous les ménages mais ne prennent pas en compte l'ensemble des indicateurs (chômage, pauvreté, sécurité alimentaire, prévalence de certaines maladies etc.). Les politiques décentralisées au niveau des collectivités se heurtent ainsi aux manques de données pour éclairer les décisions. Ce papier propose le calcul du taux de pauvreté par commune à partir des données de l'enquête sur les conditions de vie des ménages au Sénégal (EHCVM) réalisé en 2019.
1. Revevue théorique¶
Les techniques d'estimation en petits domaines constituent d'excellentes alternatives à la collecte détaillée face à l'insuffisance de ressources financières. Ces méthodes portent sur, l'estimation directe, les modèles de niveau domaine et les modèles de niveau individuel. Une estimation directe est celle qui utilise uniquement les données du domaine pour estimer l'indicateur recheerché. Les modèles de niveau domaine utilisent des données aggrégées qui proviennent souvent d'une autre source, et permettent ainsi d'éviter le problème de confidentialité qui constitue le principal frein à l'accès aux micro-données. Le niveau individuel utilisent des données individuelles issues de sources plus exhaustives.
1.1 Estimation directes¶
Le calcul de base est celui basé sur les estimateurs de type Horvitz-Thompson (HT) ou celui de Hájek (HA) et qui restent acceptables pour des coéficients de variations inférieurs à 20%.
Dans le cadre d'une estimation directe, la valeur de $\hat{\bar{Y}}_{HT}(d)$ correspondant à la moyenne de l'indicateur par l'estimateur dans le domaine $d$: $$\hat{\bar{Y}}_{HT}(d) = \frac{\sum_{i \in s_d}w_{di}Y_{di}}{N_d}$$
L'estimateur de Hájek est donnée par: $$\hat{\bar{Y}}_{HA}(d) = \frac{\sum_{i \in s_d}w_{di}Y_{di}}{\hat{N_d}}$$
Avec: $\hat{N}_d = \sum_{i \in s_d}w_{di}$
$~~~~~~~~$ $s_d$: l'ensemble des unités du domaine $d$.
$~~~~~~~~$ $w_{di}$: le poids de l'unité $i$ du domaine $d$.
L'estimation par le calage est obtenue par la regression généralisée aux moyens d'un vecteur de variables $X_d$ qui sont liés à l'indicateur $Y$ notamment à l'interieur du domaine $d$.
1.2 Estimation indirecte¶
Les modèles de niveau domaine et individiuel utilisent des estimations indirectes assitstées ou basées sur un modèle économétrique. Ces modèlesprennent en compte l'hétérogéneité entre les domaines à travers une estimation séparée des variances. Les estimateurs qui se rapportent à ces méthodes sont la poste stratification, l'estimateur par la régression et l'estimateur composite.
Dans le cadre de la post-stratification, il est supposé que la population est divisée en $J$ post-strates de taille $N^1, N^2, ..., N^3$, de même que dans chaque domaine $d$ avec une taille correspondante $N^j_d, j= 1, 2, ..., J$. $$\hat{\bar{Y}}_{HA}(d) = \frac{1}{N_d}\sum_{j = 1}^J N_d^j\hat{Y}_j$$
L'estimation de niveau domaine est donnée réalisée sur la base d'une valeur aggrégée $X_d$ d'un vecteur de variables pour tous les individus dudit domaine $d$:
$$Y_d = X_d \beta_d + \epsilon_d$$Dans le cadre du modèle de niveau individuel, l'estimation est faite sur la base de valeurs individelles $X_{di}$ d'un vecteur de variables de l'observation $i$:
$$Y_{di} = X_{di} \beta_d + \epsilon_{di}$$La litérature présente plusieurs modèles d'estimation sous petits domaines. Par exemple, les modèles proposés par Fay et Herriot (1979), sont des modèles linéaires largement répandus pour l’estimation sur petits domaines sont largement utlisés dans la pratique.
Il existe des modules informatiques associés à des logiciels statistiques pour la pratique des méthodes d'estimation sur petits domaines. Dans ce document, le logiciel Stata est utilisé pour illustrer la mise en pratique d'une méthode de désaggregation des indicateurs de pauvreté.
2. Préparation des données
La technique d'estimation sur petits domaine qui est utilisée ici porte sur un modèle de niveau individuel. Elle requiert donc en plus de la base d'enquête sur laquelle porte l'étude, une base mère qui correspond aux données du recensement général de la population. Les bases de données sont disponible sur l'Archivage national des Données du Sénégal, accessible via la plateforme https://anads.ansd.sn sur laquelle les utilisateurs peuvent s'inscrire.
2.1 Données d'enquête sur la pauvreté¶
Les données utilisées ici sont celles issues de l'Enquête Harmonisée sur les Conditions de Vie des Ménages de 2018 (EHCVM-2018) du Sénégal, chargée en mémoire ci-après.
ls *.dta
14.5M 2/09/24 18:09 ehcvm_conso_SEN2018.dta 4884.1k 2/09/24 18:09 ehcvm_individu_SEN2018.dta 375.1k 2/09/24 18:09 ehcvm_menage_SEN2018.dta 637.7k 2/09/24 18:09 ehcvm_welfare_SEN2018.dta 3573.2M 2/23/24 10:25 spss_car_individu_10eme_dr v3.dta
* Chargement de la base individus
use ehcvm_individu_SEN2018, clear
L'importance de prendre réside sur la présence de la variable relative au département. Ainsi, les variables portants sur l'identification du ménages, la région, le département et le milieu de résidence sont extrites pour les ramener au niveau ménages en supprimant les doublons indituis par la prise en compte des membres du ménages.
* Prise en compte du département
quietly {
keep hhid region departement milieu
duplicates drop hhid, force
}
La base en mémoire étant ramenée au niveau ménage, elle est fusionnée à la base d'analyse de la pauvreté qui elle également porte sur les ménages afin de récupérer les variables relatives au poids, à la taille, au seuil de pauvreté et au bien-être du ménage.
* Fusion avec la base portant sur l'analyse de la Pauvreté
merge 1:1 hhid using ehcvm_welfare_SEN2018, nogenerate nolabel ///
keepusing(grappe hhweight hhsize zref pcexp)
Result Number of obs
-----------------------------------------
Not matched 0
Matched 7,156
-----------------------------------------
De même, dans la base portant sur les ménages, les variables relatives aux caratéristiques de l'habitat sont récupérées.
* Fusion avec la base portant sur l'analyse de la Pauvreté
merge 1:1 hhid using ehcvm_menage_SEN2018, nogenerate nolabel ///
keepusing(logem mur toit sol toilet elec_ac cuisin tv frigo ordin fer car)
Result Number of obs
-----------------------------------------
Not matched 0
Matched 7,156
-----------------------------------------
Une fois la notre base d'étude est constituée, la variable qui identifie la pauvreté est créée ci-après afin de déterminer les pauvres et les non pauvres. La variable zref est une constante qui porte sur le seuil de pauvreté.
* Définition de la Variable indiquant la pauvreté
label define pauv 0 "Non Pauvre" 1 Pauvre
generate pauv:pauv = pcexp < zref
label variable pauv "Indicatrice de pauvreté"
La pauvreté étant calculée au niveau des individus, le poids utilisé est donc celui qui prends en compte le ménage (poids du ménage hhweight) et ses membres (taille du ménage hhsize). La population totale (variable pop) est obtenue à partir du premier élément de la matrice de sortie de la commande total. Le nombre total de DR de la base de sondage est définie par ndr.
* Calcul du poids des individus et total population
global ndr = 17164 // Nombre total de DR
quietly {
generate poids = hhweight * hhsize
total poids
global TOT = r(table)[1,1]
generate pop = $TOT
generate ndr = $ndr
}
Le plan de sondage est fait suivant un tirage des DR suivant le milieu de résidence, puis un tirage des ménages par DR (voir le rapport). Ce plan de sondage est déclaré ci-après.
* Le code : 1rrDdmmmm
generate menid = (1000 + departement) * 10000 + _n, after(hhid)
format menid %8.0f
generate depid = 1000 + departement, after(menid)
* Déclaration du plan de sondage
svyset grappe, strata(milieu) fpc(ndr) || _n [pw = poids], fpc(pop)
Sampling weights: poids
VCE: linearized
Single unit: missing
Strata 1: milieu
Sampling unit 1: grappe
FPC 1: ndr
Strata 2: <one>
Sampling unit 2: <observations>
FPC 2: pop
* Données d'enquête EHCVM 2018
save mysurvey, replace
(file mysurvey.dta not found) file mysurvey.dta saved
* Total par département dans la base EHCVM
quietly {
generate un = 1
collect clear
collect create deptabEHCVM
collect: svy: total un, over(departement)
collect style cell, nformat(%5.2f)
collect style showbase off
collect layout (colname) (result)
}
2.2 Données de recensement¶
La base mère porte sur les données du Recensement général de la Population, de l'Habitat, de l'Agriculture et de l'Elevage de 2013 (RGPHAE-2013). La est fournie au format sav (SPSS) et le chargement en mémoire est effectué ci-dessous.
* Importation de la base RGPHAE 2013 (partie Habitat)
import spss using "spss_habitat_10eme_dr v2.sav", clear
* Identification des variables explicatives
rename (A01 A02 E13_2 E13_4 E13_12 E13_16 E14_1)(region departement tv frigo ordin fer car)
quietly{
recode E03 (1 2 = 1)(3 4 5 = 2)(6 7 8 = 3), generate(logem)
generate mur = E05 > 5
generate toit = inlist(E06, 1,2,3)
generate sol = inlist(E07, 1,2,5,6,7)
generate toilet = E08 < 22
generate elec_ac = E11 == 1
generate cuisin = inlist(E12, 3, 4)
}
(77 vars, 145,952 obs)
* Identification des départements et des ménages
keep region departement logem mur toit sol toilet elec_ac cuisin tv frigo ordin fer car
replace departement = 10 * region + departement if departement < 10
generate menid = (1000 + departement) * 10000 + _n, before(region) // Le code : 1rrDmmmm
format menid %8.0f
generate depid = 1000 + departement, after(menid) // Le code : 1rrD
variable departement was byte now int (145,952 real changes made)
Le bien être des ménages est modélisé ici en fonction des caratéristiques de leur habitat. A cet effet, le type de logement ($logem$) indique la proprieté du logement en distinguant les propriétaires ayant un titre (1), ceux n'ayant pas de titre (2), les locataires (3) et les autres types de propriété (4). Cette variable est considérée ici comme continue ordinale où le premier niveau signifie une meilleure aisance et le dernier une précarité. Il y a également la nature du sol ($sol$) à savoir si celui-ci est recouvert de matériaux solides ou pas, l'accès à l'éléctricité ($elec_ac$), la dispobinibilité d'une toilette ayant un mode d'évacuation ($toilet$), d'une fer éléctrique ($fer$), d'un réfrigérateur/congélateur ($frigo$), d'une cuisinière électrique ou à gaz ($cuisin$), d'un ordinateur portable ou fixe ($ordin$) et d'une voiture ($car$).
quietly {
* Total par département dans le recensement
gen un = 1
capture collect drop deptableRGPH
collect create deptableRGPH
collect: total un, over(departement)
* Sauvegarde pour les taux par département du recensement et de l'EHCVM
collect style cell, nformat(%5.2f)
collect style showbase off
collect layout (colname) (result)
collect export tabledep.xlsx, name(deptabEHCVM) sheet(data, replace) cell(A1) noopen replace
collect export tabledep.xlsx, name(deptableRGPH) sheet(data) cell(R1) noopen modify
}
* Taille ajustée comme poids en fonctions des totaux
quietly {
generate hhsize = 54.9942667918747 if departement == 11
replace hhsize = 103.187849774122 if departement == 12
replace hhsize = 128.630119195873 if departement == 13
replace hhsize = 76.2447266569908 if departement == 14
replace hhsize = 106.83469526728 if departement == 21
replace hhsize = 30.5789587852495 if departement == 22
replace hhsize = 101.258156260216 if departement == 23
replace hhsize = 118.665685868214 if departement == 31
replace hhsize = 152.23106918239 if departement == 32
replace hhsize = 120.384178976665 if departement == 33
replace hhsize = 110.785114777618 if departement == 41
replace hhsize = 102.559646910467 if departement == 42
replace hhsize = 100.49852675887 if departement == 43
replace hhsize = 192.932699619772 if departement == 51
replace hhsize = 118.765745501285 if departement == 52
replace hhsize = 111.993256880734 if departement == 53
replace hhsize = 125.359247397918 if departement == 54
replace hhsize = 120.426728586171 if departement == 61
replace hhsize = 154.901992882562 if departement == 62
replace hhsize = 116.724681684623 if departement == 63
replace hhsize = 112.551715550636 if departement == 71
replace hhsize = 113.914192546584 if departement == 72
replace hhsize = 132.452371442836 if departement == 73
replace hhsize = 127.189338089576 if departement == 81
replace hhsize = 115.465793304221 if departement == 82
replace hhsize = 105.674993053626 if departement == 83
replace hhsize = 135.596266184884 if departement == 91
replace hhsize = 122.68607907743 if departement == 92
replace hhsize = 123.855120828539 if departement == 93
replace hhsize = 145.121541010771 if departement == 101
replace hhsize = 102.14512195122 if departement == 102
replace hhsize = 120.978630136986 if departement == 103
replace hhsize = 144.749469964664 if departement == 111
replace hhsize = 160.489064261556 if departement == 112
replace hhsize = 61.9497663551402 if departement == 113
replace hhsize = 163.079672501412 if departement == 121
replace hhsize = 149.023888888889 if departement == 122
replace hhsize = 122.576704169424 if departement == 123
replace hhsize = 104.536477987421 if departement == 124
replace hhsize = 110.052674066599 if departement == 131
replace hhsize = 64.4136774193548 if departement == 132
replace hhsize = 114.314135667396 if departement == 133
replace hhsize = 132.708393866021 if departement == 141
replace hhsize = 170.319464720195 if departement == 142
replace hhsize = 136.392431561997 if departement == 143
replace hhsize = floor(hhsize + 0.5)
save rgphae.dta, replace
}
Dans la suite, les variables pour retenus sont définies par une macro. Il faut remarquer que ces variables ont fait l'objet d'une validation préalables pour ne retenir que celles qui sont significatives dans le modèle.
* Les variables du modèles
global hhmodel sol elec_ac toilet fer frigo cuisin ordin car
capture erase rgphae_mata
sae data import, datain("rgphae.dta") varlist($hhmodel $valpha region departement hhsize) ///
area(depid) uniqid(menid) dataout("rgphae_mata")
Saving data variables into mata matrix file (13) ----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5 .............
2.3 Diagnostic des distributions des variables explicatives¶
use mysurvey.dta, clear
label define origine 1 EHCVM 2 RGPHAE
gen origine:origine = 1
append using rgphae.dta
replace origine = 2 if missing(origine)
foreach v of varlist $hhmodel {
ksmirnov `v', by(origine)
}
Two-sample Kolmogorov–Smirnov test for equality of distribution functions
Smaller group D p-value
---------------------------------------
EHCVM 0.0000 1.000
RGPHAE -0.0108 0.202
Combined K-S 0.0108 0.401
Note: Ties exist in combined dataset;
there are 2 unique values out of 153108 observations.
Two-sample Kolmogorov–Smirnov test for equality of distribution functions
Smaller group D p-value
---------------------------------------
EHCVM 0.0057 0.645
RGPHAE 0.0000 1.000
Combined K-S 0.0057 0.981
Note: Ties exist in combined dataset;
there are 2 unique values out of 153108 observations.
Two-sample Kolmogorov–Smirnov test for equality of distribution functions
Smaller group D p-value
---------------------------------------
EHCVM 0.0600 0.000
RGPHAE 0.0000 1.000
Combined K-S 0.0600 0.000
Note: Ties exist in combined dataset;
there are 2 unique values out of 153108 observations.
Two-sample Kolmogorov–Smirnov test for equality of distribution functions
Smaller group D p-value
---------------------------------------
EHCVM 0.0015 0.968
RGPHAE 0.0000 1.000
Combined K-S 0.0015 1.000
Note: Ties exist in combined dataset;
there are 2 unique values out of 152049 observations.
Two-sample Kolmogorov–Smirnov test for equality of distribution functions
Smaller group D p-value
---------------------------------------
EHCVM 0.0000 1.000
RGPHAE -0.0452 0.000
Combined K-S 0.0452 0.000
Note: Ties exist in combined dataset;
there are 2 unique values out of 152049 observations.
Two-sample Kolmogorov–Smirnov test for equality of distribution functions
Smaller group D p-value
---------------------------------------
EHCVM 0.2920 0.000
RGPHAE 0.0000 1.000
Combined K-S 0.2920 0.000
Note: Ties exist in combined dataset;
there are 2 unique values out of 153108 observations.
Two-sample Kolmogorov–Smirnov test for equality of distribution functions
Smaller group D p-value
---------------------------------------
EHCVM 0.0295 0.000
RGPHAE 0.0000 1.000
Combined K-S 0.0295 0.000
Note: Ties exist in combined dataset;
there are 2 unique values out of 152049 observations.
Two-sample Kolmogorov–Smirnov test for equality of distribution functions
Smaller group D p-value
---------------------------------------
EHCVM 0.0414 0.000
RGPHAE 0.0000 1.000
Combined K-S 0.0414 0.000
Note: Ties exist in combined dataset;
there are 2 unique values out of 152049 observations.
La distribution est identique pour les variables portant sur le type de sol, l'accès à l'éléctricité et l'utilisation d'un fer à repasser éléctrique.
2.4 Estimation des petits domaines¶
* Base d'enquêtes pour les estimations directes
clear all
use mysurvey, clear
Le coéficient de variation (CV) est le rapport de l'écart-type par la moyenne. Il mesure la dispersion autour de la moyenne et indique la précision d'une estimation. $$\mbox{CV}(X) = \frac{\sqrt{\mbox{Var}(X)}}{\mu_X}$$
Ci-après, le taux de pauvreté est évalué ainsi que le coéficient de variation associé.
svy: mean pauv, noheader cformat(%9.4f)
estat cv
(running mean on estimation sample)
--------------------------------------------------------------
| Linearized
| Mean std. err. [95% conf. interval]
-------------+------------------------------------------------
pauv | 0.3778 0.0136 0.3511 0.4045
--------------------------------------------------------------
------------------------------------------------
| Linearized
| Mean std. err. CV (%)
-------------+----------------------------------
pauv | .3777714 .0135892 3.59721
------------------------------------------------
Le taux de pauvreté ainsi estimé est conforme à la valeur indiquée dans le rapport de l'EHCVM-2019. De même, les taux de pauvreté par région sont illustrés ci-après.
* Evaluation du taux de pauvreté par région et cv (en %)
svy: mean pauv, over(region) noheader cformat(%9.4f)
(running mean on estimation sample)
---------------------------------------------------------------
| Linearized
| Mean std. err. [95% conf. interval]
--------------+------------------------------------------------
c.pauv@region |
DAKAR | 0.0905 0.0161 0.0589 0.1220
ZIGUINCHOR | 0.5107 0.0424 0.4274 0.5941
DIOURBEL | 0.4390 0.0461 0.3485 0.5295
SAINT-LOUIS | 0.4014 0.0469 0.3093 0.4936
TAMBACOUNDA | 0.6189 0.0372 0.5458 0.6920
KAOLACK | 0.4150 0.0468 0.3231 0.5069
THIES | 0.3411 0.0456 0.2516 0.4305
LOUGA | 0.4340 0.0423 0.3509 0.5172
FATICK | 0.4925 0.0484 0.3974 0.5876
KOLDA | 0.5657 0.0359 0.4952 0.6362
MATAM | 0.4767 0.0437 0.3909 0.5625
KAFFRINE | 0.5302 0.0521 0.4279 0.6325
KEDOUGOU | 0.6194 0.0470 0.5270 0.7118
SEDHIOU | 0.6561 0.0284 0.6003 0.7120
---------------------------------------------------------------
* Calcul des coéfficients de variation
estat cv
------------------------------------------------
| Linearized
Over | Mean std. err. CV (%)
-------------+----------------------------------
c.pauv@|
region |
DAKAR | .0904756 .0160752 17.7674
ZIGUINCHOR | .5107458 .0424332 8.30808
DIOURBEL | .4390148 .0460848 10.4973
SAINT-LOUIS | .4014224 .0469228 11.6891
TAMBACOUNDA | .61891 .0372374 6.01662
KAOLACK | .4150012 .0467858 11.2736
THIES | .3410758 .0455527 13.3556
LOUGA | .4340283 .0423396 9.75503
FATICK | .4924895 .0484233 9.83234
KOLDA | .5656942 .0358749 6.34175
MATAM | .4766939 .0437058 9.16852
KAFFRINE | .5302031 .0520877 9.82411
KEDOUGOU | .6193946 .0470415 7.59476
SEDHIOU | .6561378 .0284487 4.33578
------------------------------------------------
Une autre mesure de la precision d'un estimateur est l'erreur quadratique moyen (Mean squared Error - MSE) qui est la somme de la variance et du carré du biais: $$\mbox{MSE}(X) = \mbox{VAR}(X) + (X - \hat{X})^2$$
Dans la literrature, la qualité d'une estimation est jugée satisfaisante lorsque le coéfficient de variation est inférieure à 20%. Cependant, le MSE est le meilleure instrument de la qualité d'une estimation. Le coéfficient de variation est également approché par le rapport de la racine du MSE par la valeur de l'estimation: $$\mbox{CV}(X) \approx \frac{\sqrt{\mbox{MSE}(X)}}{\hat{X}}$$
Nous pouvons estimer l'incidence (fgt0), la profondeur (fgt1) et la Sévérité (fgt2) de la pauvreté qui sont des indicateurs classe Foster-Greer-Thorbecke d'ordre $\alpha$ (fgt$\alpha$): $$ fgt\alpha = \frac{1}{N}\sum_{h=1}^{N}\left(\frac{z-x_h}{z}\right)^{\alpha}I(x_h \leq z)$$
* Indicateurs de pauvreté: incidence, profondeur et sévérité
preserve
sp_groupfunction [pw = poids], poverty(pcexp) povertyline(zref) by(region)
quietly replace value = value * 100 if value < 1
table region measure, statistic(mean value) nformat(%9.1f)
restore
---------------------------------------------
| measure
| fgt0 fgt1 fgt2 Total
----------------+----------------------------
Group by region |
DAKAR | 9.0 1.4 0.4 3.6
ZIGUINCHOR | 51.1 15.5 6.5 24.3
DIOURBEL | 43.9 10.6 3.6 19.4
SAINT-LOUIS | 40.1 11.1 4.2 18.5
TAMBACOUNDA | 61.9 19.6 8.1 29.8
KAOLACK | 41.5 11.9 4.9 19.4
THIES | 34.1 7.7 2.5 14.7
LOUGA | 43.4 11.3 4.0 19.6
FATICK | 49.2 13.0 4.5 22.2
KOLDA | 56.6 16.3 6.3 26.4
MATAM | 47.7 14.6 6.1 22.8
KAFFRINE | 53.0 16.8 7.3 25.7
KEDOUGOU | 61.9 22.1 10.6 31.5
SEDHIOU | 65.6 21.6 9.1 32.1
Total | 47.1 13.8 5.6 22.2
---------------------------------------------
Les estimations sur les taux de pauvretés par région sont statistiquement acceptable\footnote{Ces taux de pauvreté par région correspondent aux valeurs présentées dans le rapport de l'EHCVM-2018}
L'estimation directe est possible pour certains départements dans la mesure où le CV indique une estimatimation précise. En guise d'exemple, les taux de pauvreté de certains départements sont illustrés ci-après.
* Evaluation du taux pour les départements des régions n° 1 et 11 (Dakar et Matam)
quietly svy, subpop(if inlist(region,1 ,7, 11, 13)): mean pauv, over(departement) noheader cformat(%9.4f)
estat cv
------------------------------------------------
| Linearized
Over | Mean std. err. CV (%)
-------------+----------------------------------
c.pauv@|
departement |
DAKAR | .0291363 .0132225 45.3814
PIKINE | .1321421 .0282022 21.3423
RUFISQUE | .0934209 .0380717 40.7528
GUEDIAWAYE | .0979538 .0498916 50.9338
M’BOUR | .2687416 .0809952 30.1387
THIES | .3146007 .0611424 19.4349
TIVAOUANE | .488583 .081349 16.65
MATAM | .3811586 .0571363 14.9902
KANEL | .6261479 .0558915 8.92624
RANEROU | .292417 .0815452 27.8866
KEDOUGOU | .5382443 .0621747 11.5514
SALEMATA | .8035799 .0448803 5.58505
SARAYA | .7184072 .0807631 11.242
------------------------------------------------
Il ressort des résultats ci-haut que les départements de Thiès ($cv = 19,4\%$), Tivaouane ($cv = 16,7\%$), Matam ($cv = 15,0\%$), Kanel ($cv = 8,9\%$), Kédougou ($cv = 11,6\%$), Salémata ($cv = 5,6\%$) et Saraya ($cv = 11,2\%$) présentent de bonnes qualité des estimations du taux de pauvreté avec des niveaux de précisions acceptables.
Pour les départements de Dakar, Pikine, Rifisque, Guédiawaye, Mbour et Ranérou, les valeurs sont statistiquement iréalistes et ne peuvent faire l'objet de publication. C'est sans doute l'une des raisons pour lesquelles les indicateur de pauvreté ne sont pas produits au niveau des départements. Cependant, en utilisant les données de recensement, il est possible d'augmenter la précision des indicateurs au niveau des départements.
Le modèle implémenté ici est semblable à un modèle multiniveaux. En effet, le modèle inclut les effets propres aux départements et se présente comme suit:
$$Y_{id} = X_{id}\beta + \eta_d + \epsilon_{id}$$$$\eta_d \sim N(0,\sigma_{\eta}^2)$$$$\epsilon_{id} \sim N(0,\sigma_{\epsilon}^2)$$
Avec $\eta = (\eta_d)$ et $\epsilon = (\epsilon_{id})$ les erreurs indépendantes et identiquement distribuées respectivement au niveau département $d$ et du ménage $i$ au sein du département $d$.
* Les variables du modèles
global hhmodel sol elec_ac toilet fer frigo cuisin ordin car
* Implementation du modèle
sae model h3 pcexp $hhmodel [aw=poids], area(depid) alfatest(residus)
You chose H3, parameters must be obtained via bootstrap I changed it for you.
WARNING: 0 observations removed due to less than 3 observations in the cluster.
OLS model:
------------------------------------------------------------------------------
pcexp | Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
car | 429386.5 51753.2 8.30 0.000 327952.1 530820.9
cuisin | 559242.7 72933.67 7.67 0.000 416295.4 702190.1
elec_ac | 65767.58 9713.253 6.77 0.000 46729.95 84805.2
fer | 282897 73973.26 3.82 0.000 137912 427881.9
frigo | 115384.9 13773.92 8.38 0.000 88388.48 142381.2
ordin | 162026.9 26724.43 6.06 0.000 109648 214405.9
sol | 53928.77 7576.331 7.12 0.000 39079.44 68778.11
toilet | 73129.95 9021.931 8.11 0.000 55447.29 90812.61
_cons | 279307 5295.191 52.75 0.000 268928.6 289685.3
------------------------------------------------------------------------------
GLS model:
------------------------------------------------------------------------------
pcexp | Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
car | 426887.7 35078.91 12.17 0.000 358134.3 495641.1
cuisin | 460835.3 42262.94 10.90 0.000 378001.4 543669.1
elec_ac | 49933.06 15567.44 3.21 0.001 19421.44 80444.69
fer | 248032.6 44234.63 5.61 0.000 161334.3 334730.9
frigo | 87845.37 16962.33 5.18 0.000 54599.81 121090.9
ordin | 128029.6 24361.11 5.26 0.000 80282.71 175776.5
sol | 41339.71 15173.38 2.72 0.006 11600.42 71078.99
toilet | 43540.64 15695.66 2.77 0.006 12777.71 74303.58
_cons | 317364.1 19643.75 16.16 0.000 278863.1 355865.2
------------------------------------------------------------------------------
Comparison between OLS and GLS models:
----------------------------------------
Variable | bOLS bGLS
-------------+--------------------------
car | 429386.51 426887.66
cuisin | 559242.73 460835.27
elec_ac | 65767.577 49933.065
fer | 282896.96 248032.59
frigo | 115384.86 87845.374
ordin | 162026.94 128029.61
sol | 53928.771 41339.707
toilet | 73129.946 43540.644
_cons | 279306.96 317364.14
----------------------------------------
Model settings
-------------------------------------------------------------
Error decomposition H3
Beta model diagnostics
-------------------------------------------------------------
Number of observations = 7156
Adjusted R-squared = .33572098
R-squared = .33646371
Root MSE = 367776.67
F-stat = 453.00953
Model parameters
-------------------------------------------------------------
Sigma ETA sq. = 8.450e+09
Ratio of sigma eta sq over MSE = .06247223
Variance of epsilon = 1.276e+11
-------------------------------------------------------------
<End of first stage>
Le model ci-haut est globalement significatif et toutes les variables explicatives sont également significatives. Pour illustrer la validation du modèle, le residus sauvegardé dans la variable residus sera étudié.
* calculates the residuals
predict residual, stdp
pnorm residual // P-P plot
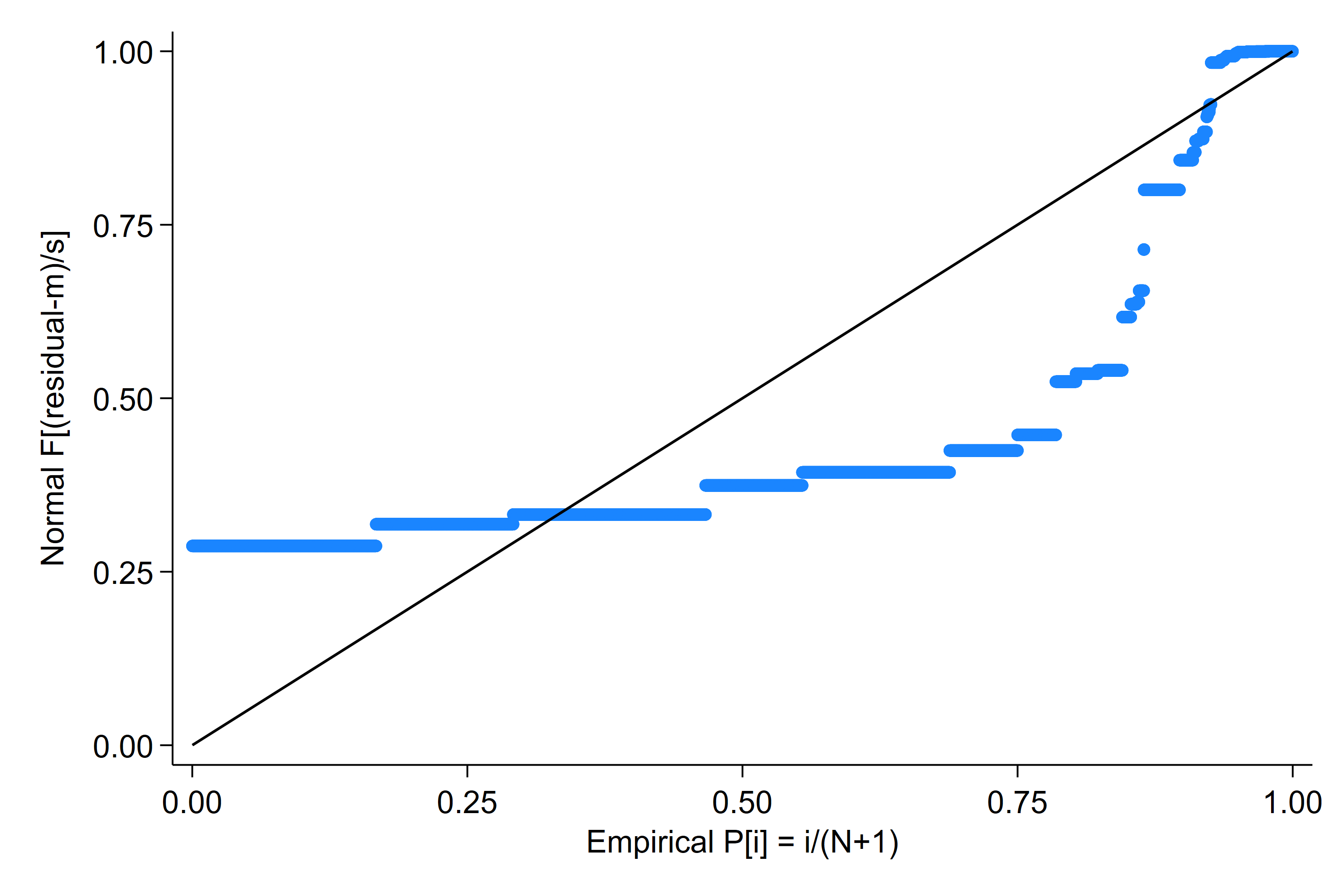
* Test de normalité de Kolmogorov
quietly summarize residual
ksmirnov residual = normal((residual-r(mean))/r(sd))
One-sample Kolmogorov–Smirnov test against theoretical distribution
normal((residual-r(mean))/r(sd))
Smaller group D p-value
---------------------------------------
residual 0.3376 0.000
Cumulative -0.2871 0.000
Combined K-S 0.3376 0.000
Note: Ties exist in dataset;
there are 83 unique values out of 7156 observations.
sktest residual
Skewness and kurtosis tests for normality
----- Joint test -----
Variable | Obs Pr(skewness) Pr(kurtosis) Adj chi2(2) Prob>chi2
-------------+-----------------------------------------------------------------
residual | 7,156 0.0000 0.0000 . .
* Calcul des taux de pauvreté au niveau région: help sae_mc_bs
capture erase reg_ind.dta
sae sim h3 pcexp $hhmodel [aw=poids], area(region) mcrep(100) bsrep(200) lnskew ///
matin("rgphae_mata") seed(648743) pwcensus(hhsize) indicators(fgt0 fgt1 fgt2) aggids(0 4) ///
uniqid(menid) plines(333440.5) ydump("reg_ind") addvars(region departement)
Transform | k [95% conf. interval] Skewness
-----------------+--------------------------------------------------
ln(pcexp-k) | 63855.32 (not calculated) -.0000596
You chose H3, parameters must be obtained via bootstrap I changed it for you.
WARNING: 0 observations removed due to less than 3 observations in the cluster.
OLS model:
------------------------------------------------------------------------------
__00000V | Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
car | .4387514 .0598563 7.33 0.000 .3214353 .5560675
cuisin | .4988222 .0612204 8.15 0.000 .3788324 .6188119
elec_ac | .1967789 .0237207 8.30 0.000 .1502871 .2432707
fer | .2381771 .0610403 3.90 0.000 .1185404 .3578138
frigo | .2695088 .0252759 10.66 0.000 .2199689 .3190487
ordin | .2865358 .0322105 8.90 0.000 .2234044 .3496672
sol | .2076757 .0269136 7.72 0.000 .1549261 .2604254
toilet | .2459095 .0230942 10.65 0.000 .2006458 .2911733
_cons | 12.13309 .0242458 500.42 0.000 12.08557 12.18061
------------------------------------------------------------------------------
GLS model:
------------------------------------------------------------------------------
__00000V | Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
car | .4465231 .0564968 7.90 0.000 .3357914 .5572547
cuisin | .4228272 .0672037 6.29 0.000 .2911103 .5545441
elec_ac | .1554233 .0249109 6.24 0.000 .1065989 .2042477
fer | .1997791 .0713912 2.80 0.005 .0598549 .3397033
frigo | .240401 .0272886 8.81 0.000 .1869163 .2938856
ordin | .2464834 .0394653 6.25 0.000 .1691329 .3238339
sol | .1895094 .0242499 7.81 0.000 .1419804 .2370384
toilet | .1691187 .0248695 6.80 0.000 .1203754 .2178621
_cons | 12.20642 .0423069 288.52 0.000 12.1235 12.28934
------------------------------------------------------------------------------
Comparison between OLS and GLS models:
----------------------------------------
Variable | bOLS bGLS
-------------+--------------------------
car | .43875142 .44652306
cuisin | .49882217 .42282721
elec_ac | .1967789 .1554233
fer | .23817707 .19977909
frigo | .26950883 .24040099
ordin | .2865358 .24648338
sol | .20767572 .18950942
toilet | .24590952 .16911873
_cons | 12.133092 12.206424
----------------------------------------
Model settings
-------------------------------------------------------------
Error decomposition H3
Beta model diagnostics
-------------------------------------------------------------
Number of observations = 7156
Adjusted R-squared = .36547947
R-squared = .36618892
Root MSE = .58944326
F-stat = 516.15385
Model parameters
-------------------------------------------------------------
Sigma ETA sq. = .0165475
Ratio of sigma eta sq over MSE = .04762646
Variance of epsilon = .33435174
-------------------------------------------------------------
<End of first stage>
file C:\Users\ADMINI~1\AppData\Local\Temp\ST_5e18_000002.tmp saved as .dta
format
Number of observations in target dataset:
145952
Number of clusters in target dataset:
14
Number of simulations: 100
Each dot (.) represents 1 simulation(s).
----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5
.................................................. 50
.................................................. 100
1 2
+-----------------------------+
1 | region departement |
+-----------------------------+
Number of bootstraps: 200
----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5
.................................................. 50
.................................................. 100
.................................................. 150
.................................................. 200
* Régions
label define region 1 dakar 2 ziguinchor 3 diourbel 4 "saint louis" ///
5 tambacounda 6 kaolack 7 thies 8 louga 9 fatick 10 kolda ///
11 matam 12 kaffrine 13 kedougou 14 sedhiou 0 "Sénégal"
label values Unit region
* Calcul des CV
rename avg_fgt?* fgt?
rename mse_avg_fgt?* mse_fgt?
gen cv = sqrt(mse_Mean)/Mean
list Unit fgt0 cv, separator(0)
+------------------------------------+
| Unit fgt0 cv |
|------------------------------------|
1. | Sénégal .39152634 .0259936 |
2. | dakar .08685181 .0424283 |
3. | ziguinchor .5529409 .0350127 |
4. | diourbel .43198058 .0299098 |
5. | saint louis .40805438 .0368402 |
6. | tambacounda .61741511 .0336907 |
7. | kaolack .46511799 .0318288 |
8. | thies .31713077 .0381758 |
9. | louga .47942428 .0339875 |
10. | fatick .53022612 .0350681 |
11. | kolda .56737921 .0288719 |
12. | matam .55807362 .0345904 |
13. | kaffrine .60865975 .0316842 |
14. | kedougou .67223531 .0362578 |
15. | sedhiou .67929809 .0387472 |
+------------------------------------+
Le modèle étant validé, la simulation est réalisée ci-après. Pour assurer une reproductivité de cette simulation, une valeur du seed est fixée dans la mesure les simulation fond appel à des procédures aléatoire de boostrap et de réplication.
* Base d'enquêtes pour les estimations directes
clear all
use mysurvey, clear
* Calcul des taux de pauvreté au niveau départemental
capture erase dep_ind.dta
sae sim h3 pcexp $hhmodel [aw=poids], area(depid) mcrep(100) bsrep(200) lnskew /// zvar($valpha)
matin("rgphae_mata") seed(648743) pwcensus(hhsize) indicators(fgt0 fgt1 fgt2) aggids(0 4) ///
uniqid(menid) plines(333440.5) ydump("dep_ind") addvars(region departement)
Transform | k [95% conf. interval] Skewness
-----------------+--------------------------------------------------
ln(pcexp-k) | 63855.32 (not calculated) -.0000596
You chose H3, parameters must be obtained via bootstrap I changed it for you.
WARNING: 0 observations removed due to less than 3 observations in the cluster.
OLS model:
------------------------------------------------------------------------------
__00000Z | Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
car | .4387514 .0598563 7.33 0.000 .3214353 .5560675
cuisin | .4988222 .0612204 8.15 0.000 .3788324 .6188119
elec_ac | .1967789 .0237207 8.30 0.000 .1502871 .2432707
fer | .2381771 .0610403 3.90 0.000 .1185404 .3578138
frigo | .2695088 .0252759 10.66 0.000 .2199689 .3190487
ordin | .2865358 .0322105 8.90 0.000 .2234044 .3496672
sol | .2076757 .0269136 7.72 0.000 .1549261 .2604254
toilet | .2459095 .0230942 10.65 0.000 .2006458 .2911733
_cons | 12.13309 .0242458 500.42 0.000 12.08557 12.18061
------------------------------------------------------------------------------
GLS model:
------------------------------------------------------------------------------
__00000Z | Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
car | .4368352 .0556347 7.85 0.000 .3277931 .5458772
cuisin | .3732037 .067057 5.57 0.000 .2417743 .5046331
elec_ac | .1615472 .0247065 6.54 0.000 .1131233 .2099711
fer | .1797044 .0701477 2.56 0.010 .0422174 .3171914
frigo | .2299043 .0269068 8.54 0.000 .1771679 .2826407
ordin | .2383688 .0386122 6.17 0.000 .1626903 .3140473
sol | .1861218 .024077 7.73 0.000 .1389317 .2333119
toilet | .1459835 .0250105 5.84 0.000 .0969639 .1950031
_cons | 12.23003 .0343478 356.06 0.000 12.16271 12.29735
------------------------------------------------------------------------------
Comparison between OLS and GLS models:
----------------------------------------
Variable | bOLS bGLS
-------------+--------------------------
car | .43875142 .43683516
cuisin | .49882217 .37320373
elec_ac | .1967789 .16154722
fer | .23817707 .1797044
frigo | .26950883 .2299043
ordin | .2865358 .23836882
sol | .20767572 .18612181
toilet | .24590952 .14598347
_cons | 12.133092 12.23003
----------------------------------------
Model settings
-------------------------------------------------------------
Error decomposition H3
Beta model diagnostics
-------------------------------------------------------------
Number of observations = 7156
Adjusted R-squared = .36547947
R-squared = .36618892
Root MSE = .58944326
F-stat = 516.15385
Model parameters
-------------------------------------------------------------
Sigma ETA sq. = .02851715
Ratio of sigma eta sq over MSE = .08207712
Variance of epsilon = .32138139
-------------------------------------------------------------
<End of first stage>
file C:\Users\ADMINI~1\AppData\Local\Temp\ST_5e18_000002.tmp saved as .dta
format
Number of observations in target dataset:
145952
Number of clusters in target dataset:
45
Number of simulations: 100
Each dot (.) represents 1 simulation(s).
----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5
.................................................. 50
.................................................. 100
1 2
+-----------------------------+
1 | region departement |
+-----------------------------+
Number of bootstraps: 200
----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5
.................................................. 50
.................................................. 100
.................................................. 150
.................................................. 200
* Labélisation des départements
quietly {
label define ldep 1011 DAKAR 1012 PIKINE 1013 RUFISQUE 1014 GUEDIAWAYE, replace
label define ldep 1021 BIGNONA 1022 OUSSOUYE 1023 ZIGUINCHOR 1031 BAMBEY, add
label define ldep 1033 MBACKE 1041 DAGANA 1042 PODOR 1043 "SAINT LOUIS", add
label define ldep 1051 BAKEL 1052 TAMBACOUNDA 1053 GOUDIRY 1054 KOUMPENTOUM, add
label define ldep 1061 KAOLACK 1062 "NIORO DU RIP" 1063 GUINGUINEO 1071 MBOUR, add
label define ldep 1072 THIES 1073 TIVAOUANE 1081 KEBEMER 1082 LINGUERE, add
label define ldep 1083 LOUGA 1091 FATICK 1092 FOUNDIOUGNE 1093 GOSSAS, add
label define ldep 1101 KOLDA 1102 VELINGARA 1103 "MEDINA YORO FOULAH", add
label define ldep 1111 MATAM 1112 KANEL 1113 "RANEROU FERLO" 1121 KAFFRINE, add
label define ldep 1122 BIRKILANE 1123 KOUNGHEUL 1124 "MALEM HODAR", add
label define ldep 1131 KEDOUGOU 1132 SALEMATA 1133 SARAYA 1141 SEDHIOU, add
label define ldep 1142 BOUNKILING 1143 GOUDOMP 1032 DIOURBEL 0 "Sénégal", add
label value Unit ldep
}
* Calcul des CV
rename avg_fgt?* fgt?
rename mse_avg_fgt?* mse_fgt?
gen cv = sqrt(mse_Mean)/Mean
save estimation.dta, replace
list Unit fgt0 cv, separator(0)
+-------------------------------------------+
| Unit fgt0 cv |
|-------------------------------------------|
1. | Sénégal .39314396 .0245006 |
2. | DAKAR .0311213 .0376509 |
3. | PIKINE .11938527 .0486264 |
4. | RUFISQUE .1502926 .0595379 |
5. | GUEDIAWAYE .07491748 .0686017 |
6. | BIGNONA .67118852 .0498465 |
7. | OUSSOUYE .47948124 .0846282 |
8. | ZIGUINCHOR .43589046 .0463794 |
9. | BAMBEY .48789737 .066788 |
10. | DIOURBEL .45042373 .0599627 |
11. | MBACKE .4163025 .0389329 |
12. | DAGANA .45498736 .0501862 |
13. | PODOR .64259919 .0477666 |
14. | SAINT LOUIS .14135604 .0524266 |
15. | BAKEL .57349038 .0859424 |
16. | TAMBACOUNDA .6353023 .0487277 |
17. | GOUDIRY .61194476 .0699625 |
18. | KOUMPENTOUM .57827586 .0545797 |
19. | KAOLACK .3098309 .0340206 |
20. | NIORO DU RIP .68648483 .0597996 |
21. | GUINGUINEO .43401583 .059109 |
22. | MBOUR .29871031 .0517566 |
23. | THIES .25664946 .053947 |
24. | TIVAOUANE .43375063 .0530006 |
25. | KEBEMER .54871058 .0699852 |
26. | LINGUERE .49884207 .0482854 |
27. | LOUGA .40655568 .051157 |
28. | FATICK .52803378 .0516206 |
29. | FOUNDIOUGNE .53532003 .0526643 |
30. | GOSSAS .48036088 .0681071 |
31. | KOLDA .56186017 .0480111 |
32. | VELINGARA .52785301 .0391171 |
33. | MEDINA YORO FOULAH .64380776 .0645493 |
34. | MATAM .47403122 .0402668 |
35. | KANEL .67547387 .0560238 |
36. | RANEROU FERLO .42045526 .0610093 |
37. | KAFFRINE .53047235 .0476209 |
38. | BIRKILANE .53950562 .0662672 |
39. | KOUNGHEUL .66306506 .0616982 |
40. | MALEM HODAR .76194872 .094181 |
41. | KEDOUGOU .54707739 .0415646 |
42. | SALEMATA .82711974 .1053075 |
43. | SARAYA .82091314 .0883487 |
44. | SEDHIOU .65238636 .0624033 |
45. | BOUNKILING .67085526 .0647781 |
46. | GOUDOMP .69992718 .0577798 |
+-------------------------------------------+
use estimation.dta, clear
* Création d'un code
decode Unit, gen(unid)
replace unid = strlower(ustrtrim(stritrim(unid)))
(46 real changes made)
duplicates report unid
Duplicates in terms of unid
--------------------------------------
Copies | Observations Surplus
----------+---------------------------
1 | 46 0
--------------------------------------
drop if !Unit
(1 observation deleted)
frame rename default depart
frame create maps
cwf maps
use Maps/base_new.dta, clear
*rename NOM unid
replace unid = strlower(ustrtrim(stritrim(unid)))
(0 real changes made)
save, replace
. replace unid = "ranerou" in 36 (1 real change made) . save "estimation.dta", replace file estimation.dta saved file estimation.dta saved
edit
cwf depart
merge 1:1 unid using Maps/base_new.dta, nogen
(variable unid was str18, now str19 to accommodate using data's values)
Result Number of obs
-----------------------------------------
Not matched 1
from master 0
from using 1
Matched 45
-----------------------------------------
save pauvdata, replace
(file pauvdata.dta not found) file pauvdata.dta saved
use pauvdata, clear
* Création du de la bse de label
replace fgt0 = round(100*fgt0, .1) if fgt0 < 1
replace cv = round(100*cv, .1) if cv < 1
cap decode Unit, generate(dep)
quietly {
expand 2, gen(typs)
gen labs = dep if !typs
replace labs = string(fgt0) +"("+string(cv)+"%"+")" if typs == 1
keep id x_c y_c typs labs Unit
save pauvlab, replace
}
(45 real changes made) (45 real changes made)
use pauvdata, clear
spmap fgt0 using Maps/cord_new, id(id) fcolor(Heat) label(data(pauvlab) ///
label(labs) xcoord(x_c) ycoord(y_c) position(12 0) angle(0 0) gap(*.1 *0.5) ///
size(tiny tiny) color(black blue%80) by(typs)) clnumber(14) legenda(off) ///
title("Carte de pauvreté départementale") note("Source: Tall, 2024")
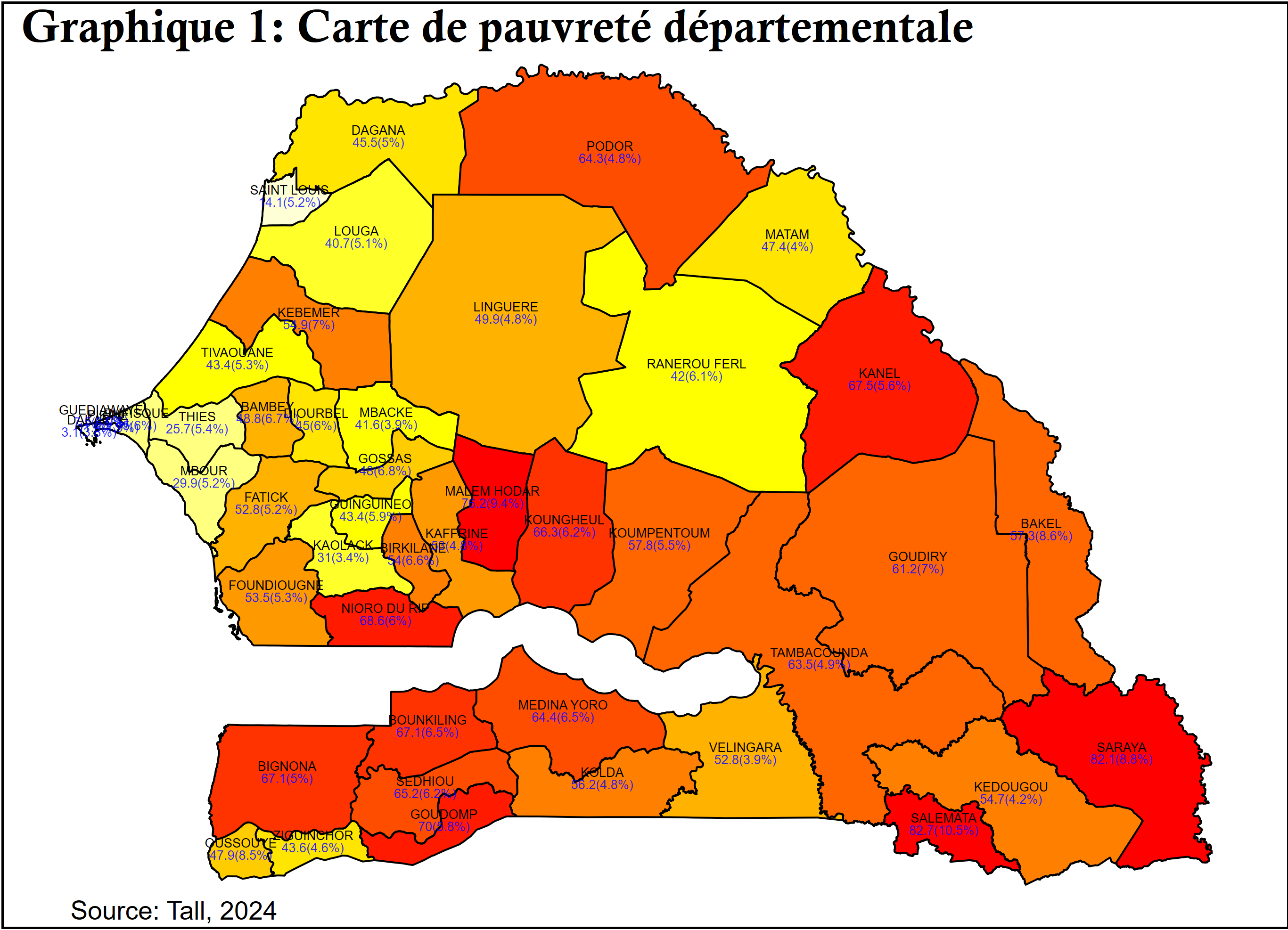
use pauvlab, clear
gen region = mod(int(Unit/10),100), before(Unit)
replace region = 1 if missing(region)
keep if region == 1
replace labs = "KEUR MASSAR" if missing(Unit) & !typs
replace labs = "??" if missing(Unit) & typs
save dklab, replace
use pauvdata, clear
gen region = mod(int(Unit/10),100), before(Unit)
replace region = 1 if missing(region)
spmap fgt0 using Maps/cord_new if region == 1, id(id) fcolor(yellow%1 yellow%5 yellow%10 yellow%20) label(data(dklab) ///
label(labs) xcoord(x_c) ycoord(y_c) position(12 0) angle(0 0) gap(*.1 *0.5) ///
size(tiny tiny) color(black blue%80) by(typs)) legenda(off) ///
title("Carte de pauvreté départementale") note("Source: Tall, 2024")
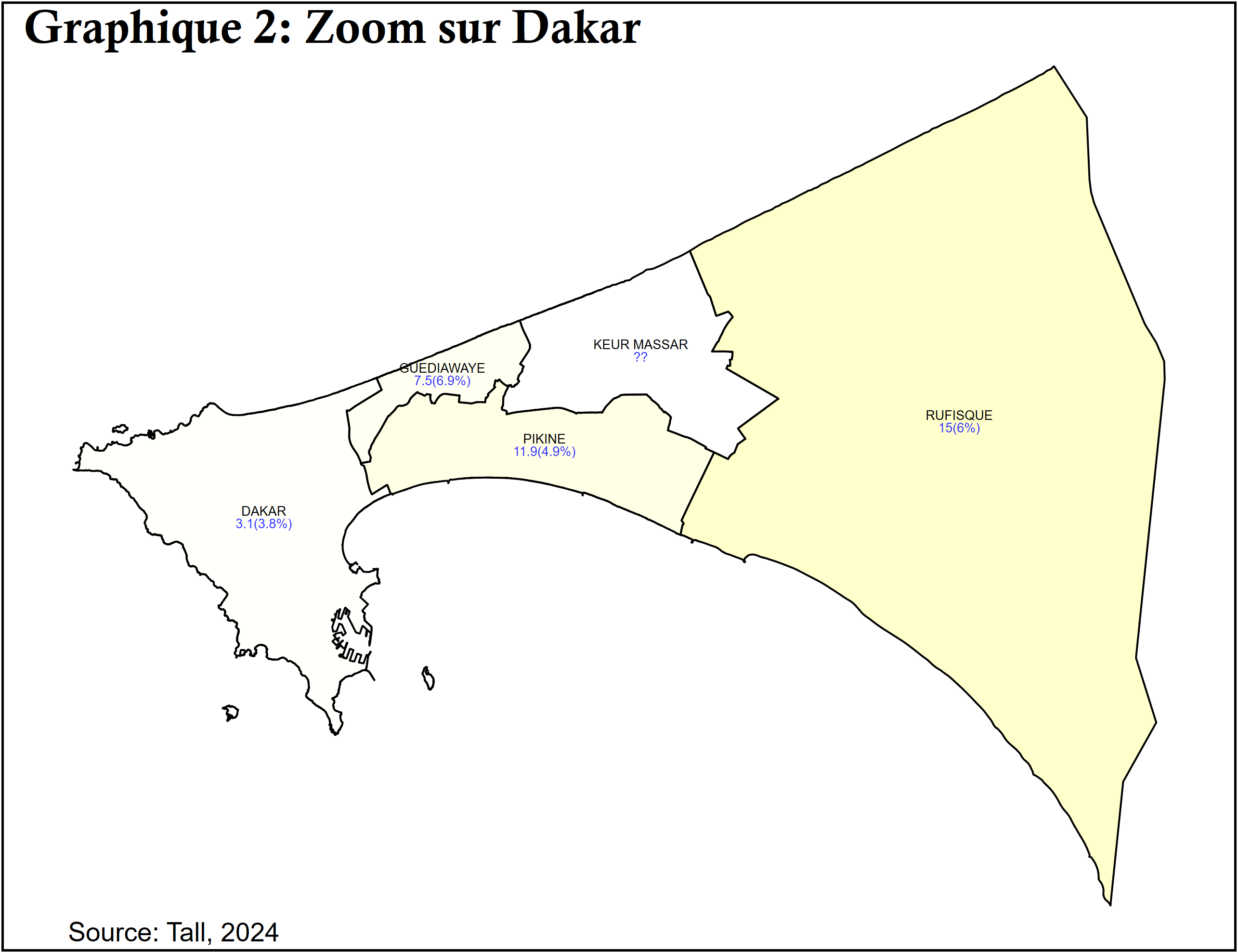
* Suppression des fichiers temporaires
foreach x in "mysurvey.dta" "rgphae.dta" "rgphae_mata" "estimation.dta" "rgph_ind" {
capture erase `x'
}
sae data export, matasource("rgph_ind") numfiles(1) datasave("rgph_indx")
use rgph_indx, clear
generate pop = 15967476
generate zref = 333440.5
replace _WEIGHT = pop/_N
* Déclaration du plan de sondage
svyset _n [pw = _WEIGHT], fpc(pop)
* Définition de la Variable indiquant la pauvreté
label define pauv 0 "Non Pauvre" 1 Pauvre
generate pauv:pauv = _YHAT1 < zref
label variable pauv "Indicatrice de pauvreté"
* Evaluation du taux de pauvreté par région et cv (en %)
qui svy: mean pauv, over(departement) noheader cformat(%9.4f)
estat cv
clear all
erase rgphae_mata